Apche Calcite查询优化概述

Aug 9 2023 Database>SQL Engine 31 minutes read (About 4641 words) VISITED TIMES

本文已收录在合集Apche Calcite原理与实践中.

本文是Apache Calcite原理与实践系列的第五篇. 经过前面几篇文章的铺垫, 本文终于开始进入Calcite中最为核心的查询优化器的介绍. 由于查询优化器所涉及的概念多且实现逻辑复杂, 后续将分几篇文章进行介绍. 本文首先介绍与查询优化相关的理论基础, 之后介绍Calcite中与查询优化相关的概念和数据结构. 后面的两篇文章将具体介绍Calcite中的两个优化器, HepPlanner和VolcanoPlanner的实现细节.

需要说明的是, 查询优化器的研究可以追溯到20世纪70年代, 有漫长的研究历史. 其本身也是一个十分复杂的问题, 本文所描述的基础理论意在后续更方便地讲解Calcite中的相关实现, 更为全面和准确的查询优化理论请参考相关论文.

查询优化基础

查询优化的目的

当前几乎所有的数据管理系统(包括传统的数据库管理系统, 以及大数据计算引擎, 如Hive, Spark, Flink等)都支持SQL访问. 而SQL是一种高级的声明式语言, 相比于命令式语言, SQL仅描述了需要的结果. 具体的执行步骤则交由数据系统决定.

尽管SQL在使用上十分方便, 然而使用SQL描述的查询或计算逻辑, 通常会有两个问题. 一是在逻辑上不是最优的, 比如不小心写入了恒等的过滤条件; 其次在物理上无法考虑底层数据存储的分布. 因此支持SQL的系统需要将原始的SQL经过解析与查询优化之后, 生成最优的执行计划并执行. 在OLTP中, 上线的SQL通常经过DBA的严格审核, 充分考虑了数据库内部的细节, 因此对查询优化器的挑战并不大. 然而在大数据时代, OLAP和大数据计算引擎大多直接面向用户, 且查询复杂度极高, 此时对查询优化器的考验就比较大了. 当前SQL已经成为了几乎所有数据管理系统的标准访问接口, 甚至连NoSQL都开始支持SQL访问, 在这背后查询优化器是不可缺少的技术.

查询优化的历史

从E. F. Codd在1970年发表关系模型的论文之后, 就有了大量关于查询优化器的研究. 下图列举了几个具有重要意义的查询优化器研究或系统. Ingres是最早的基于关系代数的数据库管理系统, 它的查询优化器以启发式的规则优化为主. System R是IBM的关系数据库研究项目, 其关于查询优化的论文提出了基于成本的优化, 以及Bottom-up的动态规划搜索算法，如今许多成熟的OLTP系统仍采用类似的优化方式, 如MySQL. Starburst主要面向逻辑优化, 提出了实现一套可扩展的规则引擎来更好的实现逻辑关系代数转换. Volcano/Cascades则是查询优化领域具有重要里程碑意义的研究, 它设计了一整套查询优化器所需的组件, 包括逻辑和物理算子, 用于关系算子转换的规则集, 物理属性, 成本模型等, 以及Top-Down风格的搜索策略. Columbia是一篇硕士论文, 注重于Volcano/Cascades风格优化器的高效实现.

目前成熟的开源查询优化器主要有Apache Calcite和GPORCA, 它们都是Volcano/Cascades风格的优化器实现, 且均可作为独立模块存在, 服务于不同的数据管理系统. 其中GPORCA采用了多线程优化搜索, 更适用于OLAP类需要低延时的系统, 例如阿里云的Hologres就使用了GPORCA作为优化器.

查询优化的原理

从用户的角度来看, 查询优化的结果就是将输入的SQL语句转化为高效的执行计划. 而从数据管理系统的角度来看, 查询优化由外到里可分为两个层次:

语义级优化: 基于SQL语法进行优化.
代数级优化: 根据关系代数的原理进行优化.

对于一个成熟的数据库管理系统或大数据计算引擎而言, 在上面所说的两个层面一般都会根据执行引擎自身的特点有相应的优化. 其中发挥重要作用的是代数级的优化, 又包括基于规则的优化(或称逻辑优化)和基于成本的优化(或称物理优化). 本文所描述的查询优化是代数级的优化, 后文所说的查询优化如果不作特殊说明均指在关系代数基础上进行的查询优化.

术语

为了更方便地进行讲述, 这里规定一些术语, 在本文及之后的文章中常会用到.

术语	含义
逻辑算子(Logical Operator)	逻辑算子是高级算子, 仅用于指定数据转换而不指定物理算法, 例如Calcite中的`LogicalJoin`
物理算子(Physical Operator)	物理算子代表了特定的物理实现算法, 如Calcite中的`EnumerableHashJoin`
查询树/查询计划(Query Tree/ Query Plan)	由逻辑算子组成的树状结构, 由SQL转换而来, 是查询优化器的输入. 在Calcite中等价于逻辑的`RelNode`树
执行计划(Execution Plan)	有物理算子组成的树状结构, 明确指示了如何执行查询, 是查询优化器的输出. 在Calcite中等价于物理的`RelNode`树
表达式(Expression)	包含一个算子以及零个或多个输入, 既可以是逻辑的也可以是物理的. 查询计划是逻辑表达式, 执行计划是物理表达式.

基础算法

基于关系代数的查询优化背后的数学原理是关系代数的等价变换, 其本质是将原始的查询计划, 通过等价变换, 转换为更低成本的执行计划. 这个变换并寻找更低成本执行计划的过程有两种算法, 一种是纯粹基于预定义规则的方法, 另一种是在规则的基础上引入成本计算, 从而可以进一步扩大搜索空间, 寻找更优的执行计划.

基于规则的优化(Rule-Based Optimization, RBO)

基于规则的优化根据指定的优化规则对关系表达式进行转换, 从而得到一种执行成本更低的查询计划. 规则的定义需要Pattern和Substitution, 其中Pattern表示规则可匹配的查询子树, 而Substitution表示与Pattern等价的关系表达式. 可供优化规则有很多, 这里仍以上一篇文章中的SQL语句为例, 列举几个常见的优化规则.

首先是投影下推(或称列裁剪), 观察下图中的原始查询计划, 可以发现整个查询树中只用到了user表的id和name列, 以及order表的user_id和price列. 我们可以将这个信息下推到Scan算子, 这样只需读取所需的4列数据即可, 如果这两个表有很多其他列就可以节省大量IO.

其次是谓词下推, 可以发现Filter算子只对order表的price列进行了过滤, 因此可以把Filter算子下推到Join算子之下, 这样可以在Join之前对order表中的数据进行过滤, 减少Join表的数据量, 提升执行效率.

基于成本的优化(Cost-Based Optimization, CBO)

基于规则的优化可应用一些一定有正向收益的规则, 比如上文所列举的投影下推, 谓词下推等. 但是基于规则的优化无法感知数据分布, 对一些问题就束手无策, 比如典型的Join重排问题. 而基于成本的优化可通过应用更多的规则变换来生成更多的备选计划, 从中根据执行成本挑选最优的查询计划.

需要注意的是, 尽管被称为基于成本的优化, 它仍然要结合规则生成多个等价的查询计划, 然后结合每个查询计划的执行成本, 挑选最优的计划. 也就是说, 无论是基于规则的优化还是基于成本的优化, 规则都是其中的核心之一, 不同之处在于: 在基于规则的优化中, 只能应用少量有明显正向收益的规则; 而在基于成本的优化中, 可以应用更多的规则, 产生更多的查询计划, 从中结合成本挑选最优的计划.

基于成本的优化有两个核心依赖, 即:

统计信息, 例如表的行数, 列索引上唯一键的数量等.
成本模型, 在单机环境下一般考虑IO, CPU, 内存成本; 在分布式环境下还需考虑网络成本.

搜索空间

由上文的描述可知, 原始的查询计划, 通过规则变换可以生成一系列等价的查询和执行计划. 我们把所有可能生成的等价查询和执行计划称为搜索空间, 查询优化的目标就是在搜索空间中找到成本最低的执行计划.

查询优化的搜索空间会随着关系数量的增长而迅速增长, 对于3个关系的连接, 在仅考虑逻辑算子的情况下, 也有12种等价的查询计划, 如果考虑连接的物理算法, 搜索空间将会进一步扩大.

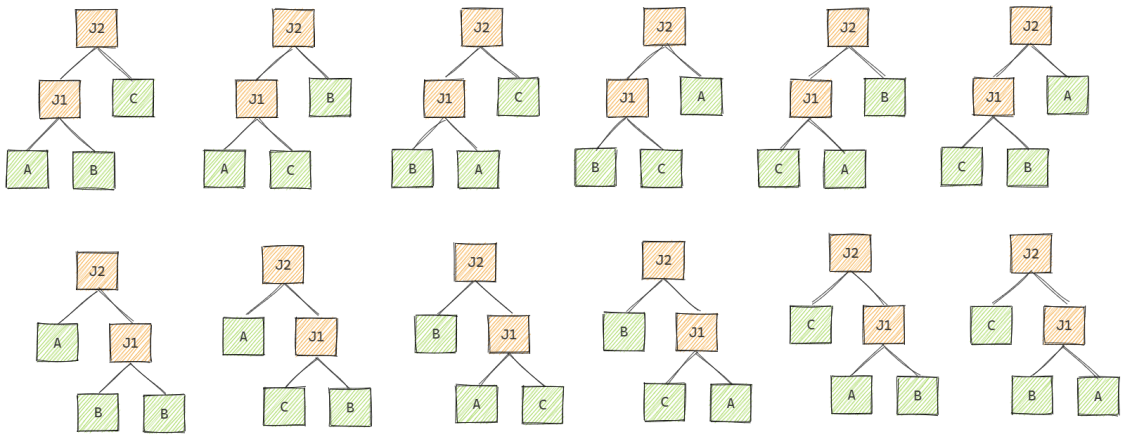
在上图中, 第一层的6棵连接树一般称为左深树, 第二层的6棵连接树一般称为右深树. 当关系数量扩展到4时还会出现稠密树, 如下图所示.

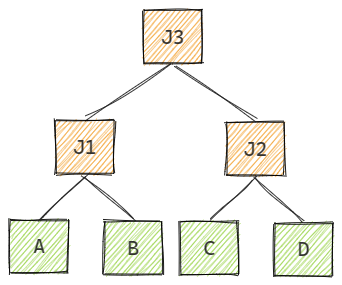
下表展示了N个关系时的逻辑搜索空间, 可以看到在仅考虑左深树的情况下, 搜索空间都呈阶乘级增长, 考虑稠密树的情况下其增长更快. 这还仅仅是考虑逻辑算子的情况, 如果考虑算子的物理实现, 搜索空间还会进一步增长. 由此可见, 查询优化的复杂度非常高, 它也被证明是NP-Hard的问题.

关系数	逻辑表达式个数	左深树个数	稠密树个数
N	$3^N-(2^{n+1}-1)+N$	$N!$	$\frac{(2N-2)!}{(N-1)!}$
1	1	1	1
2	4	2	2
3	15	6	12
4	54	24	120
5	185	120	1680
6	608	720	30240
7	1939	5040	665280
8	6058	40320	17297280
9	18669	362880	518918400
10	57012	3628800	17643225600

搜索策略

由上文我们已经知道, 查询优化是一个非常复杂的的问题, 其搜索空间巨大. 这类问题一般采用动态规划的解法, 根据请求发起的位置, 可分为Bottom-up(即从叶节点开始优化)和Top-Down(即从根节点开始优化)两种风格的优化算法. System R引入了Bottom-up风格的动态规划优化算法, 并且为了减少搜索空间引入了一些启发策略, 如只考虑左深树, 将笛卡尔积连接放到最后优化等. System R风格的优化算法对连接数较少的查询十分高效, 在OLTP中得到了广泛应用, MySQL的查询优化器整体上仍沿用这一框架. 然而对于更复杂的查询, Bottom-up的搜索算法无法进行高效的剪枝, 为此Volcano/Cascades提出了Top-Down风格的优化算法, 可以进行更高效的剪枝, 能搜索的空间也更大. 越来越多的数据库系统采用这一框架进行查询优化, 如TiDB, Greenplum等.

查询优化器

查询优化的研究经历了漫长的过程, System R最先引入了基于成本的动态规划搜索算法, 极大地推动了查询优化的研究. 但是查询优化器的实现仍非常复杂, 直到Volcano/Cascades的出现, 不仅提出了一套新的搜索算法, 还提供了一整套可扩展的查询优化器实现, 基于这个框架, 如果要对查询优化器进行扩展, 只需提供额外的算子和对应的优化规则即可, 无需再关注规则的应用顺序以及优化算法的执行流程.

Calcite查询优化器实现

Calcite提供了完整的查询优化器实现, 其中包括完全基于规则的优化器HepPlanner, 以及基于成本的优化器VolcanoPlanner, 在实现上它们都继承于RelOptPlanner. 其中VolcanoPlanner经过多次迭代, 从1.24版本开始已经支持Volcano/Cascades风格的Top-Down搜索算法.

查询优化器相关概念和数据结构

Calcite中, 与查询优化器相关的实现引入了大量的概念和数据结构, 理解这些概念和数据结构是理解优化器执行流程的关键. 本文先介绍HepPlanner与VolcanoPlanner中通用的概念和数据结构, 后续在详细介绍各个优化器的实现时, 还会介绍其独有的概念和数据结构.

RelOptRule

通过前文的介绍我们知道, 无论是RBO还是CBO, 实际都是由规则驱动的. 在Calcite中规则由RelOptRule表示, 它是目前所有规则的顶层基类, 不过最终它将被RelRule取代, 新实现的规则建议都继承RelRule.

Calcite中已经实现了上百种优化规则, 从优化内容来看可以分为以下两种类型:

TransformationRule: 用于将一种逻辑表达式转换为另一种等价的逻辑表达式. 对应Cascades中的Transformation Rule, 是一个独立的接口, 并不继承于RelOptRule. 需要注意的是TransformationRule接口仅在VolcanoPlanner中有效, HepPlanner会直接忽略这一接口.
ConverterRule: 用于将一种Calling Convention的表达式转换为另一种Calling Convention的表达式, 可用于将逻辑表达式转换为物理表达式. 对应Cascades中的Implementation Rule, ConverterRule继承于RelOptRule.

Calcite中还有一个用于标识规则种类的接口SubstitutionRule, 它继承于TransformationRule, 在VolcanoPlaner中使用, 用于标识一定有正收益的规则, 后续会进一步介绍.

定义一个规则至少需要两部分信息, 即Pattern和Sustitution, 在Calcite中:

Pattern由RelOptRuleOperand实现, 用于表示该规则可匹配的表达式结构.
Substitution表示该规则可产生的逻辑等价表达式, 在函数onMatch()中实现.

TransformationRule仅涉及到逻辑算子的转换, FilterMergeRule是一个简单的TransformationRule案例, 它将查询树中的上下两个Filter算子合并为一个. 规则触发的逻辑实现在onMatch()方法中, 在Config接口中通过RelOptRuleOperand定义了规则的Pattern.

/** Planner rule that combines two LogicalFilters */
@Value.Enclosing
public class FilterMergeRule extends RelRule<FilterMergeRule.Config> implements SubstitutionRule {

  /** Creates a FilterMergeRule. */
  protected FilterMergeRule(Config config) {
    super(config);
  }

  @Override public void onMatch(RelOptRuleCall call) {
    final Filter topFilter = call.rel(0);
    final Filter bottomFilter = call.rel(1);

    final RelBuilder relBuilder = call.builder();
    relBuilder.push(bottomFilter.getInput())
        .filter(bottomFilter.getCondition(), topFilter.getCondition());

    call.transformTo(relBuilder.build());
  }

  /** Rule configuration. */
  @Value.Immutable
  public interface Config extends RelRule.Config {
    Config DEFAULT = ImmutableFilterMergeRule.Config.of().withOperandFor(Filter.class);

    @Override default FilterMergeRule toRule() {
      return new FilterMergeRule(this);
    }

    /** Defines an operand tree for the given classes. */
    default Config withOperandFor(Class<? extends Filter> filterClass) {
      return withOperandSupplier(b0 ->
          b0.operand(filterClass).oneInput(b1 ->     // 匹配Filter类型且仅有一个子节点的
              b1.operand(filterClass).anyInputs()))  // 其子节点也必须为Filter类型, 支持任何输入
          .as(Config.class);
    }
  }
}

ConverterRule可用于在逻辑算子和物理算子之间进行转换, 基类的onMatch()方法会调用子类的convert()方法实现转换.

/**
 * Abstract base class for a rule which converts from one calling convention to
 * another without changing semantics.
 */
@Value.Enclosing
public abstract class ConverterRule extends RelRule<ConverterRule.Config> {
    @Override public void onMatch(RelOptRuleCall call) {
    RelNode rel = call.rel(0);
    if (rel.getTraitSet().contains(inTrait)) {
      final RelNode converted = convert(rel);
      if (converted != null) {
        call.transformTo(converted);
      }
    }
  }
}

/**
 * Rule to convert a {@link LogicalFilter} to an {@link EnumerableFilter}.
 * You may provide a custom config to convert other nodes that extend {@link Filter}.
 *
 * @see EnumerableRules#ENUMERABLE_FILTER_RULE
 */
class EnumerableFilterRule extends ConverterRule {
  /** Default configuration. */
  public static final Config DEFAULT_CONFIG = Config.INSTANCE
      .withConversion(LogicalFilter.class, f -> !f.containsOver(),
          Convention.NONE, EnumerableConvention.INSTANCE,
          "EnumerableFilterRule")
      .withRuleFactory(EnumerableFilterRule::new);

  protected EnumerableFilterRule(Config config) {
    super(config);
  }

  @Override public RelNode convert(RelNode rel) {
    final Filter filter = (Filter) rel;
    return new EnumerableFilter(rel.getCluster(),
        rel.getTraitSet().replace(EnumerableConvention.INSTANCE),
        convert(filter.getInput(),
            filter.getInput().getTraitSet()
                .replace(EnumerableConvention.INSTANCE)),
        filter.getCondition());
  }
}

RelOptRuleCall

在Calcite中, RelOptRuleCall代表一个规则的触发, 其实现关系如下图所示. 其中HepRuleCall用于HepPlanner, VolcanoRuleCall用于VolcanoPlanner. VolcanoRuleCall进一步有两个实现类, 在VolcanoPlanner的初始及优化过程中, 如果发现查询子树与某个规则匹配, 则会创建一个DeferringRuleCall, 在它的onMatch()方法中会创建一个VolcanoRuleMatch并放入队列中等待优化.

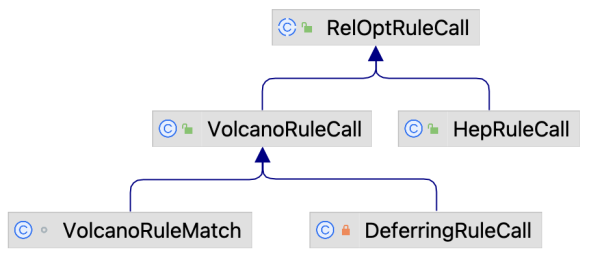
RelOptRuleCall.rels保存了与规则匹配的RelNode节点, 例如对于上文中的FilterMergeRule, 在其onMatch()方法中传入的RelOptRuleCall是一个长度为2的数组, 第一个元素是一个Filter节点, 第二个元素是第一个元素的子节点, 且仍为Filter节点.

public abstract class RelOptRuleCall {
  ...
  public final RelNode[] rels;
  ...
}

总结

本文首先介绍了与SQL查询优化相关的基础理论, 随后介绍了Calcite中的查询优化器及不同优化器间通用的概念和数据结构. 本文并不涉及任何实现细节, 核心是想厘清查询优化要解决的问题, 只有理解了这一点才能掌握查询优化器的本质. 后续的文章将在本文的基础上, 深入查询优化器的实现细节.

参考

[1] Access path selectionin arelational database management system
[2] Thevolcano optimizer generator: Extensibilityandefficient search
[3] The cascades framework for query optimization
[4] Efficiency in the Columbia Database Query Optimizer
[5] Orca: A Modular Query Optimizer Architecture for Big Data
[6] Introduction to the Join Ordering Problem
[7] Rule-based Query Optimization
[8] What is Cost-based Optimization?
[9] 数据库挖矿系列-优化器设计探索穿越之旅
[10] 揭秘TiDB新优化器: Cascades Planner原理解析

#Apache Calcite